Checking parentheses balance using Stack!

Checking for balanced parentheses or balanced brackets is a very old and classic problem in the field of computer science.

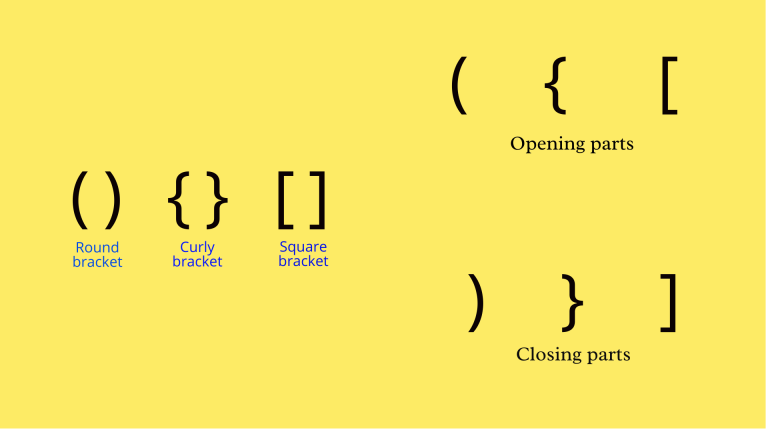
Types of parentheses

As we all know there are three kinds of parentheses or brackets. They are the round brackets, the curly brackets and the square brackets. Each of the brackets has an opening part and a closing part.

What is balanced parentheses

Now the question arises — what are balanced parentheses? Some parentheses are called balanced if each opening bracket has a corresponding closing bracket or each closing bracket has a corresponding opening bracket and the brackets are properly nested. Followings are some examples of balanced parentheses:

()
()()()
((()))
{()}
[[[]]]
[][]()(){()}{}

And the followings are some example of parentheses which are not balanced:

()))
)))(((
{()()
[[[}}}
{}{

Algorithm to balance parentheses

Now, let’s try to make an algorithm with the stack. But why stack? To understand this, we have to pay a closer look at the parentheses balancing. Some parentheses are balanced only if there is a corresponding closing part of a specific parenthesis’s opening part in sequence. Consider a string of balanced parentheses as “[{()}]”. Here, the opening parentheses are “[{(”. So to be balanced “)” has to come first, then “}” and “]” respectively. If we add the opening parts to the stack, it’ll be done as follows:

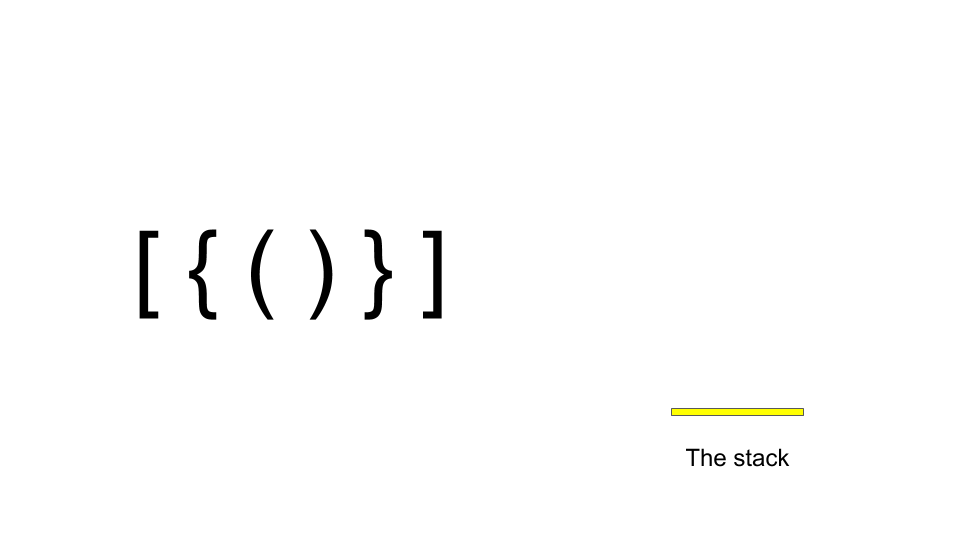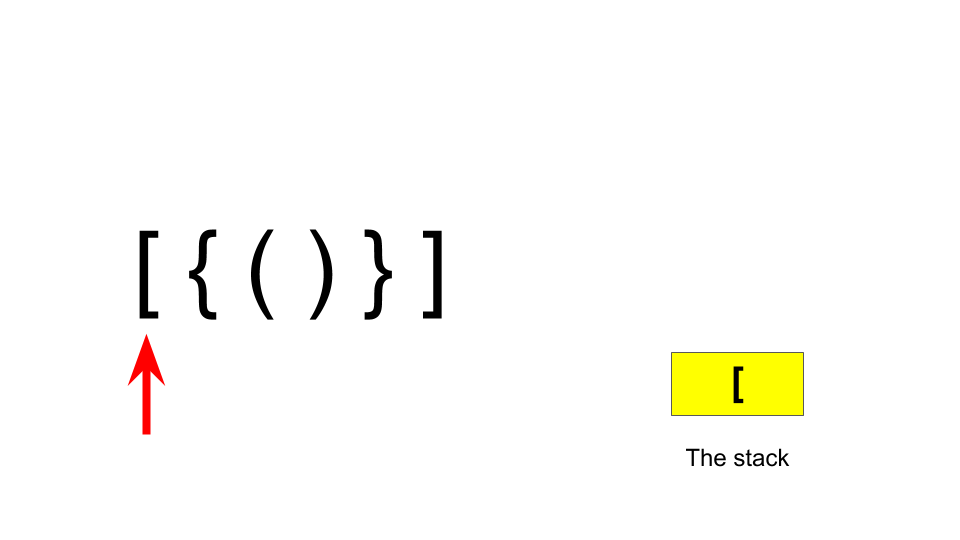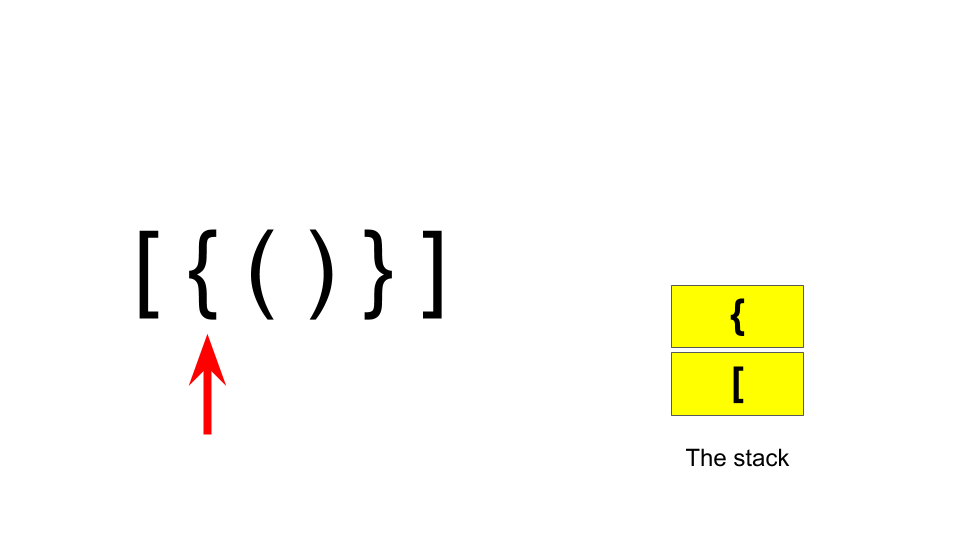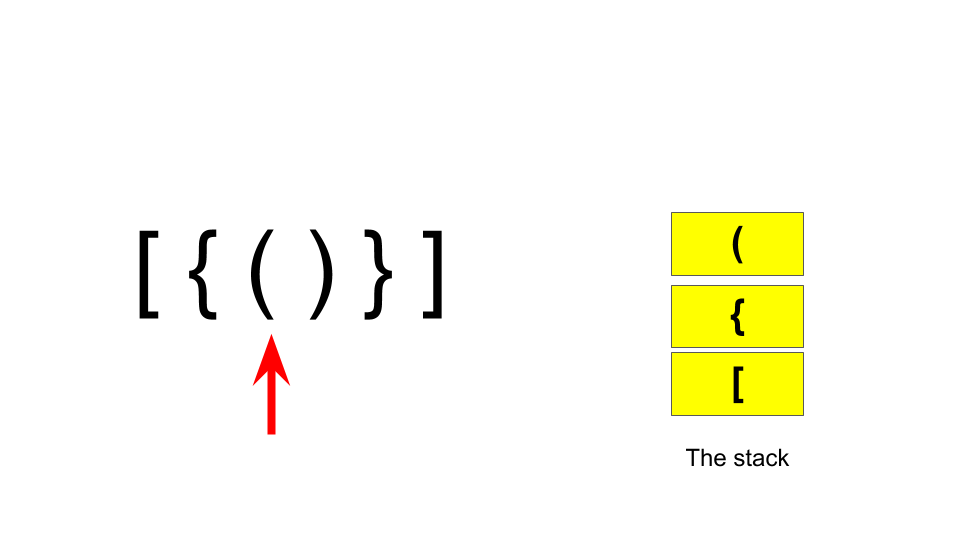
Now, when the closing part comes, if it matches the corresponding opening part, it indicates that it is a balancing part and the parenthesis is removed from the stack. It works as follows:

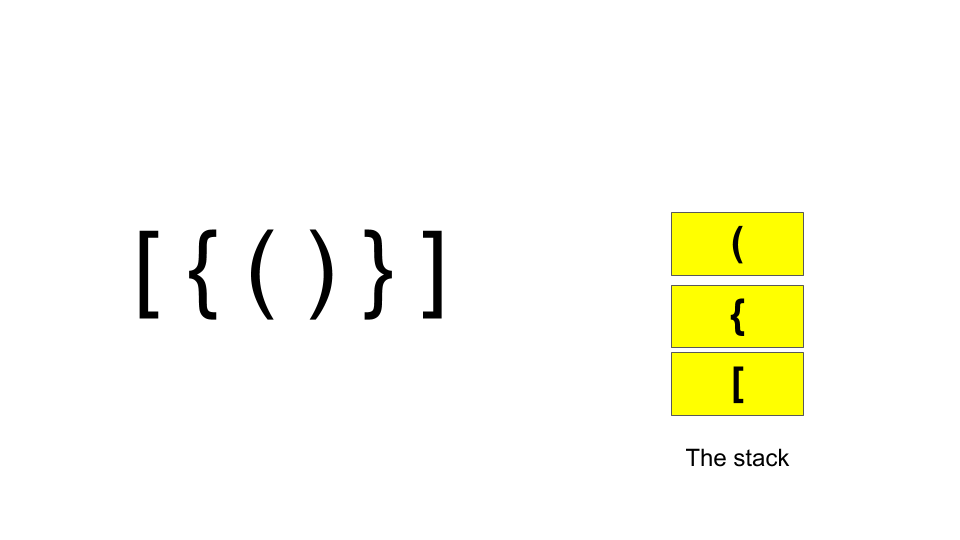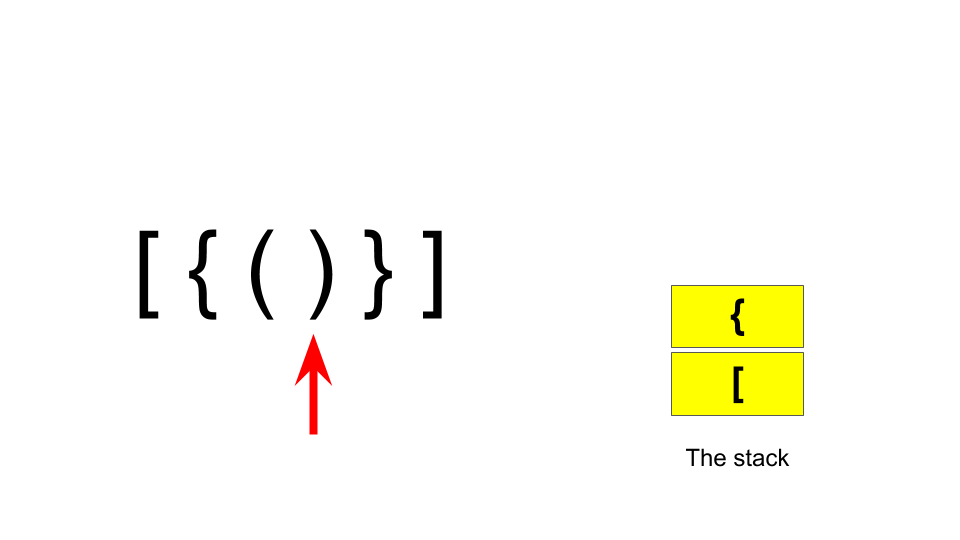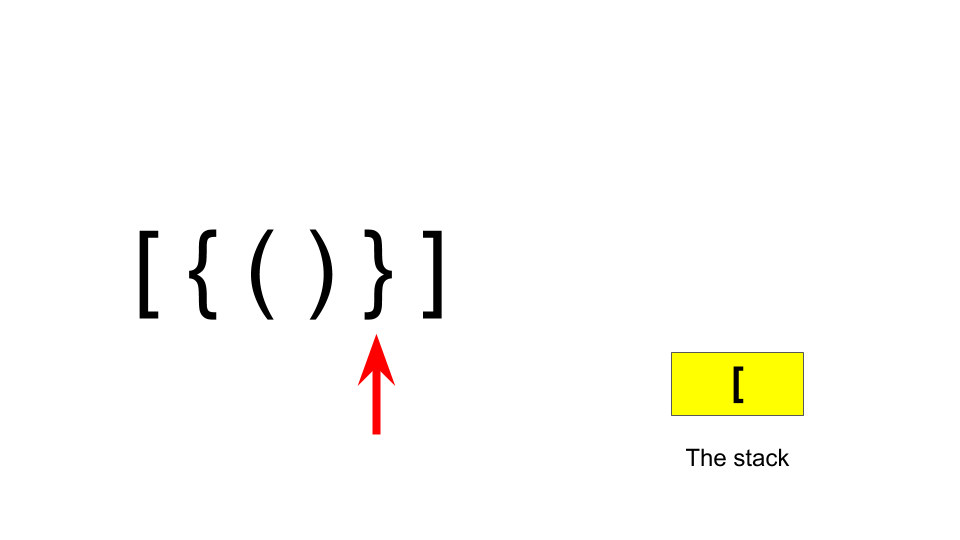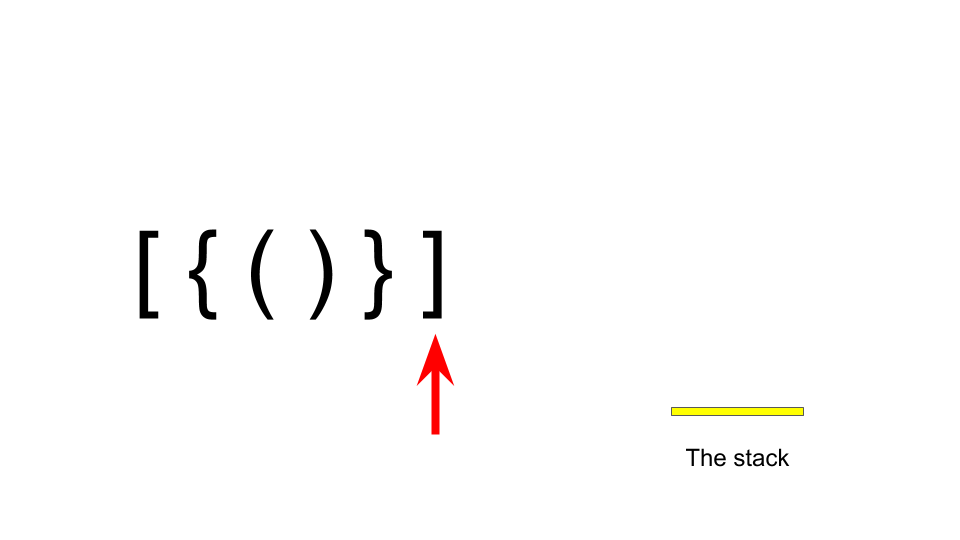
Thus if after processing the string if the stack is empty, the parentheses are balanced.

Implementation

A CPP implementation of checking parentheses balance is as follows:

bool isBalanced(string expression){
    stack <char> s;
    
    for(int i = 0; i < expression.length(); i++){
        if(expression[i] == '(' || expression[i] == '{' || expression[i] == '['){
            s.push(expression[i]);
            continue;
        }

        if(s.empty())
            return false;
        
        char c = s.top();

        switch(expression[i]){
            case ')':
                if(c != '(')
                    return false;
    
                break;

            case '}':
                if(c != '{')
                    return false;

                break;
            
            case ']':
                if(c != '[')
                    return false;

                break;
            
            default:
                break;
        }

        s.pop();
    }

    return s.empty();
}

You can get the full implementation here. If you like a video version. Check here. Thank you very much.